| Code | Material | Diameter | Focal length | Irregularity | Coating | Unit Price | Delivery | Cart |
|---|---|---|---|---|---|---|---|---|
| 1108-001 | UV Fused Silica | 6.0mm | -6mm | λ/4 | Uncoated | flash sale | 1 Week | |
| 1108-002 | UV Fused Silica | 6.0mm | -12mm | λ/4 | Uncoated | flash sale | 1 Week | |
| 1108-003 | UV Fused Silica | 9.0mm | -9mm | λ/4 | Uncoated | flash sale | 1 Week | |
| 1108-004 | UV Fused Silica | 9.0mm | -18mm | λ/4 | Uncoated | flash sale | 1 Week | |
| 1108-005 | UV Fused Silica | 12.7mm | -15mm | λ/4 | Uncoated | flash sale | 1 Week | |
| 1108-007 | UV Fused Silica | 12.7mm | -25mm | λ/4 | Uncoated | flash sale | 1 Week | |
| 1108-009 | UV Fused Silica | 12.7mm | -30mm | λ/4 | Uncoated | flash sale | 1 Week | |
| 1108-011 | UV Fused Silica | 12.7mm | -50mm | λ/4 | Uncoated | flash sale | 1 Week | |
| 1108-012 | UV Fused Silica | 25.4mm | -25mm | λ | Uncoated | flash sale | 1 Week | |
| 1108-014 | UV Fused Silica | 25.4mm | -50mm | λ/2 | Uncoated | flash sale | 1 Week | |
| 1108-016 | UV Fused Silica | 25.4mm | -75mm | λ/2 | Uncoated | flash sale | 1 Week | |
| 1108-018 | UV Fused Silica | 25.4mm | -100mm | λ/2 | Uncoated | flash sale | 1 Week |
A biconcave lens or double concave lens is an optical lens with two identical inward-bent spherical surfaces with equal radii of curvature. A double concave lens has a negative focal length and diverges a collimated light beam to the virtual focal point (that is the point at which the extension lines of the diverging light path intersect at the object side of the concave lens). The usages of Biconcave lenses are diverse, encompassing divergence of collimated or focused light beams, beam diameter modulation (e.g., Galilean beam expanders), the correction of spherical aberration of optical assemblies, and increasing the focal lengths of a lens group, etc. Due to its symmetric structure, a double concave lens works best when the conjugate ratio (object distance: image distance) is close or equal to 1:1. In such situations, the distortion, spherical/chromatic aberration, and coma could be offset as a result of the equilibrium of the lenses. Whilst, when the intended magnification ratio is <1/5 or >5, a plano concave lens will be a better alternative.
This page features North Optics’s Off-the-shelf UV Fused Silica Double Concave Lenses.
UV Fused Silica, equivalently known as JGS1, is an optical glass material with exception transmittance to the UV wavelengths, meanwhile also being widely transparent to visible and NIR wavelengths (transmission range 200-2200 nm). UV Grade Fused Silica is one of the best ultraviolet-transmitting media. The thermal properties of UVFS are prominent, too, including high-temperature endurance and low thermal expansion. Other benefits of UV-fused silica lenses encompass few bubbles/striae, high homogeneities, chemical inertness, mechanical hardness, and advantages of birefringent properties. Therefore, the UVFS lens is a superior option for building a stable optical device under harsh working conditions.
North Optics’s stock UV Fused Silica Bi-concave Lenses only have uncoated versions so far. While custom V-coatings that exhibit optimized transmission and low-cost MgF2 AR coatings with various transmission wavelengths could be furnished onto UVFS biconcave lenses upon request. Besides the stocked N-BK7 and UV Fused Silica Biconcave lenses, North Optics also provides Standard N-BK7 biconcave lenses and custom biconcave lenses made from BaF2, CaF2, MgF2, Ge, ZnSe, Sapphire, and other optical materials.
Application Notes:
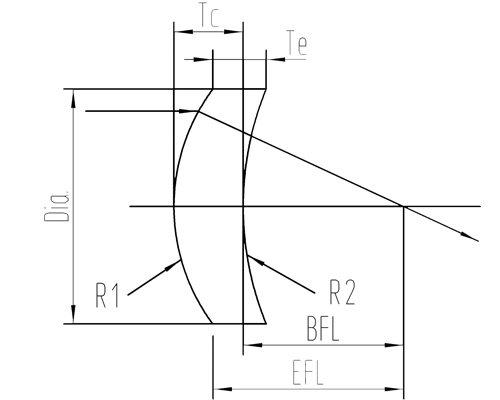
1. A biconcave lens diverges collimated light beam according to a virtual focal point on the same side as the object, therefore its focal lengths are regarded as negative. The formula to calculate the focal length of the biconcave lens can be stated as 1/f=(n-1)[1/r1-1/r2+(n-1)d/nr1r2], where f is the focal lens of the biconcave lens, n stands for the refractive index, r1, r2 are the curvature radii, and d is the thickness of the lens.
![]()
Specifications:
| Type | Biconcave Lenses | Material | UV Fused Silica(JGS1) |
| Clear Aperture | >90% | Diameter Tolerance | +0.00/-0.1mm |
| Thickness Tolerance | ±0.1mm | Surface Irregularity | λ/4-λ @ 633 nm |
| Centering Error | 3 arcmin | Focal Length Tolerance | +/-1% |
| Chamfer | 0.2mm x 45 degree |
There are various classifications of optical lenses, and either as a user or an engineer, one needs to evaluate the pros and cons of lens classifications in order to optimize the optical system. First, What is a lens? An optical lens is a transparent optical component that converges or diverges light emitted from a peripheral object. The transmitted light then forms a real or virtual image of the object. Optical lenses can be divided into three major categories: convex lenses, and concave lenses. Convex lenses have positive focal length and focus light, whilst concave lenses have negative focal length and expand collimated light beam. Further subdivided, it can be classified into the plano-convex lens, plano-concave lens, double-convex lens, double-concave lens, meniscus lens, ball/half-ball lens, achromatic doublet lens, cylindrical plano-convex lens/plano-concave lens, rod lens, aspheric lens, etc. This article enumerates the different lens classifications, exploring their characteristics, and the appropriate context to use them.
The focal length is the length from the optical center to the point where light parallel light beam converges on the optical axis. A convex lens has a positive focal lens, and a concave lens has a negative focal lens and focuses light into a virtual focal point. The conjugate ratio is defined as the ratio of the object distance (the distance between the object and the lens on the optical axis) and the image distance (the distance between the image and the lens on the optical axis). Light paths from the object to the image are reversible. An object placed at the focal point of a lens results in an infinite conjugate ratio, while an object placed at twice the focal length results in an image formed at twice the focal length, giving a conjugate ratio of 1:1.
Note: You might want to learn more about the basic concepts relevant to lens selection, such as Field of View (FOV), Image Distortion, Spherical Aberration and Coma: Spherical aberrations, etc. see our Lens Selection Tutorial. Or if you are looking for a reference to the selection of the substrate materials, see our Optical Substrate Material Selection Guide.
A Plano-convex (PCX) lens is an optical lens with one plane face and one convex face, and a positive focal length, utilized for collecting, focusing collimated lights, collimating lights from a point source, or reducing the focal length of a lens group. Compared to Biconvex lenses, Plano-convex lenses have two unidentical sides and therefore work best for an infinite absolute conjugate ratio (objective distance: image distance). However, plano-convex lenses still reduce spherical aberrations to a quite low extent when the absolute conjugate ratio is greater than 5:1. For conjugate ratio below 5:1, consider using plano-convex lenses in pairs or a biconvex lens. Plano-convex lenses are mainly used for monochromatic light, such as lasers; Plano-convex lens is often used to converge parallel light or convert point light sources into parallel light. when using the lens to focus collimated lights, the collimated lights should be projected to the curved surface of the lens.
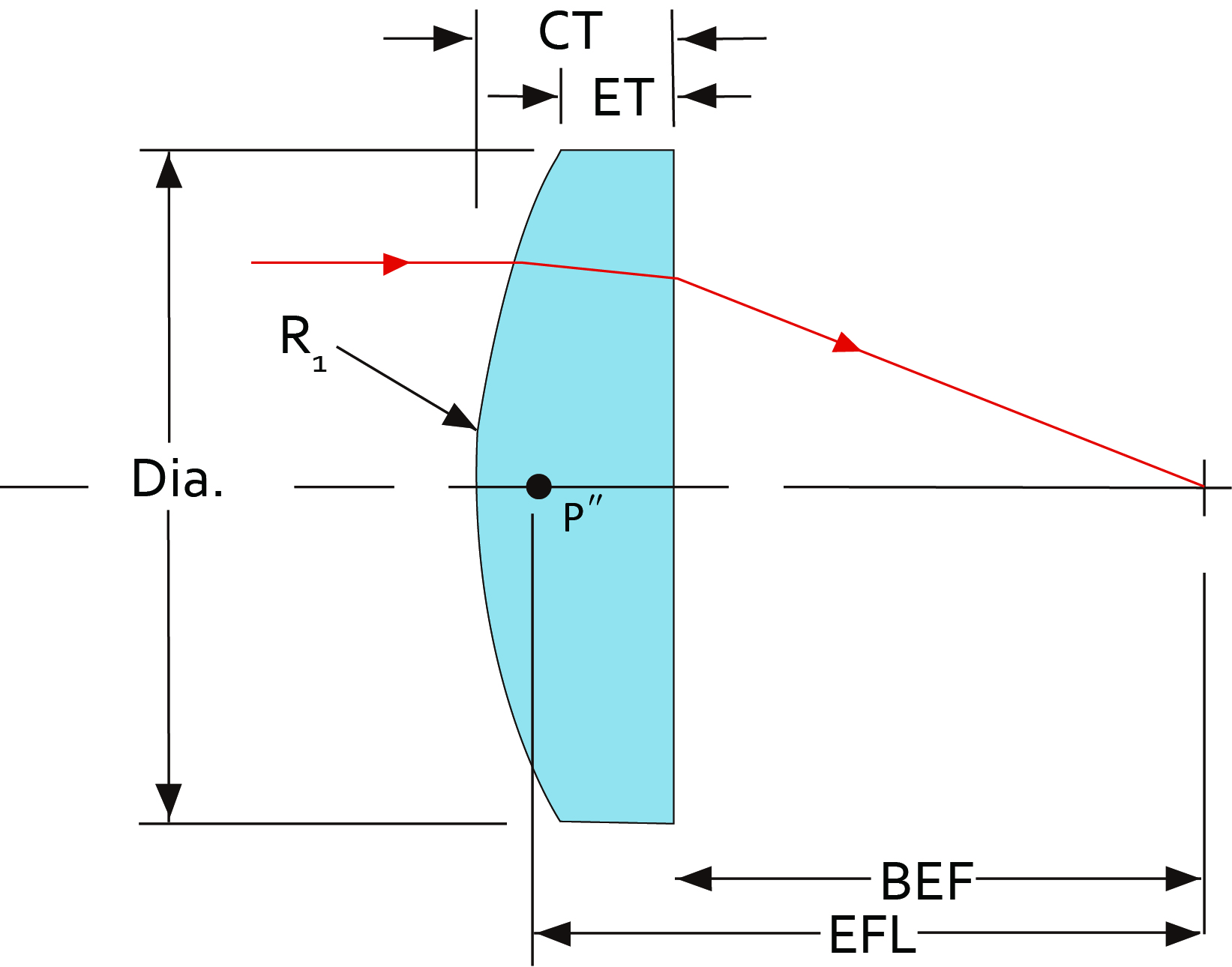
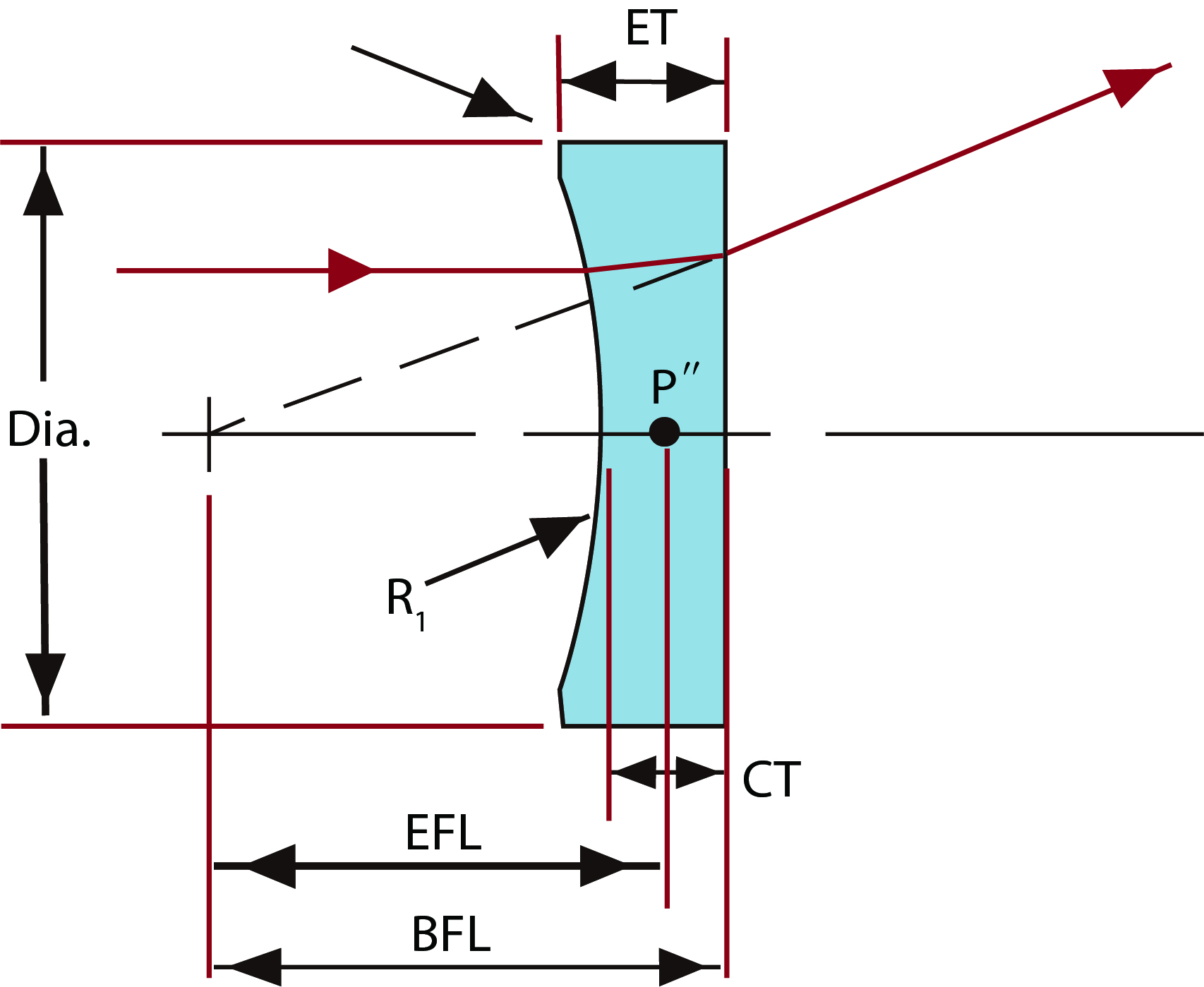
A plano-concave lens is a lens with one side flat and a concave side. A plano-concave lens has a negative focal length, which diverges the beam. Therefore, it can be utilized in to expand the beam, project light and lengthen the focal length of the optical system. Plano-concave lenses are often incorporated into Galilean beam expanders, also as components to increase the focal length of an optical instrument, or balance out the spherical aberration, improving image qualities. When the absolute conjugate ratio is greater than 5:1 (that is, the absolute value of objective distance: image distance), a plano-concave lens is the best type of negative lens to decrease spherical aberration, coma, and distortion. When applied to diverge a collimated light beam, the curved surface should face the light source (Or in other words, the flat side should point to the focal plane you intend to modulate) so that light bends gradually and spherical aberration is reduced to the greatest extent.
A Biconvex Lens, also known as a Double Convex Lens, is an optical lens with two spherical sides that have the same curvature radii. The major uses of Biconvex lenses include laser beam modulation, light focus, and imaging. Biconvex lenses have positive focal lengths and converge collimated light to a point. When the absolute finite conjugate ratio is equal to or near 1:1, biconvex lenses are advised. When the object distance and image distance are equivalent in absolute terms, biconvex lenses are the best option for conjugate ratios between 1:5 and 5:1. If not, plano-convex lenses are preferable since their asymmetric shapes help to reduce spherical aberrations. The focal lengths of the biconvex lenses could be calculated using the formula: f= (R1*R2)/((n-1)*(R2-R1)). Their curvatures on both sides are equal and are often used to gather light from a point source or transmit images to other optical systems. Since the object distance and the image distance are equivalent or approximately equivalent, distortion can be minimized.
![]()
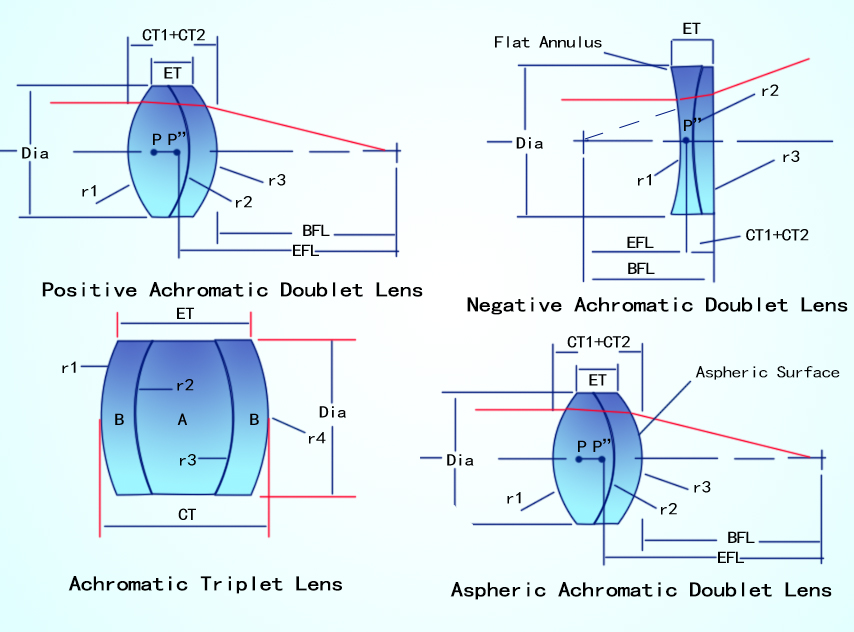
A Biconcave Lens or Double Concave Lens are optical lens with two inward-bent spherical surfaces of identical radii of curvature. A double concave lens has a negative focal length and diverges a collimated light beam to the virtual focal point (that is the point at which the extension lines of the diverging light path intersect at the object side of the concave lens) and increases the focal lengths of a lens group. The usages of Biconcave lenses are diversified, encompassing divergence of collimated or focused light beams, and beam diameter modulation (e.g. Galilean beam expanders), and because of their negative focal lengths, bi-concave lenses could also be applied in the correction of spherical aberration of optical assemblies. Due to its symmetric structure, a double concave lens works best when the conjugate ratio (object distance: image distance) is close or equal to 1:1. In such situations, the distortion, spherical/chromatic aberration, and coma could be offset as a result of the equilibrium of the lenses. Whilst, when the intended magnification ratio is <1/5 or >5, a plano concave lens will be a better alternative.
![]()
A Meniscus Lens or a Convex-concave Lens is an optical lens consisting of one concave and one convex side, and the two sides have different radii of curvature according to which the meniscus lenses could be categorized into two kinds: positive meniscus lenses and negative meniscus lenses. A Positive Meniscus Lens is more curved on the convex side than on the concave side, and its edge thickness is greater than its central thickness, contributing to a positive focal length. In contrast, a Negative Meniscus Lens is more curved on the concave side than on the convex side, and its central thickness is greater than its edge thickness, contributing to a negative focal length. Positive Meniscus Lenses converge light is utilized to reduce the focal length when used in conjunction with other lenses and increase the numerical aperture (NA) of existing optical modules without introducing significant spherical aberration. These functions are quite useful for image instruments to increase the resolution, and for focusing lasers to shrink the spot diameter when the incident beam width is rather large, providing diffraction-limited performance and better precision for laser processing. A negative meniscus lens diverges light and functions in just the opposite manner as a positive meniscus lens, to increase the focal length, reduce the NA of the optical assemblies, and expand beams. The meniscus lens is often hired as a corrective lens, and can also be used as a beam condenser of an illumination system. In addition, meniscus lenses with appropriate thicknesses can also eliminate chromatic aberration.
An Achromatic Doublet Lens is a bulk optical element, often consisting of two cemented concave and convex single lenses made from different optical glass materials of compensating dispersion properties. Achromatic doublet lens has the distinctive feature of inducing minimizing chromatic aberration in an optical module (Chromatic aberration is the shift of refractive indices resulting from different wavelengths when the incident light source consists of multi-colored radiations, the consequence is blurring of spots on the focal plane). It is also possible to correct the spherical and on-axis comatic aberration using achromatic doublet lenses.
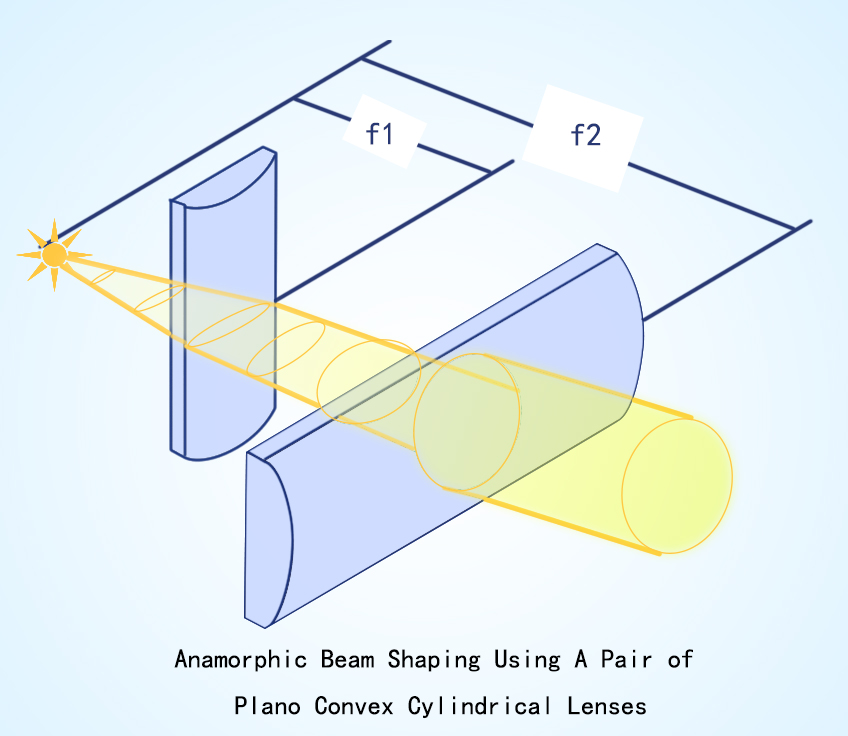
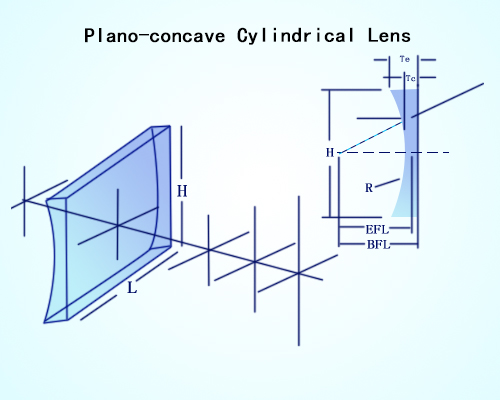
A Plano Convex/concave Cylindrical Lens is, in essence, a cuboid with an outward extending/inward curved structure, and thus a positive effective length. The fundamental function of the plano-convex cylindrical lens is to condense/diverge a matrix of laser beams and modulate the aspect ratio of the image. As a plate version of a plano-convex/concave lens, a plano-convex/concave cylindrical lens performs better at infinite conjugate ratios (here we refer to the absolute value, and the value becomes disadvantageous when below 5:1). What discriminates a plate PCX/PCV and a cylindrical PCX/PCV is that the former diverges lights in two dimensions, the later expands light beam in one.
The prior nature of plano-convex/concave cylindrical lenses, which is making a two-dimensional light beam becomes a linear laser line, can be leveraged in diversified applications like the coupling of a slit input of laser diodes, changing the aspect ratio of an image, laser scanners, dye lasers, spectroscopies, and receivers of energies in linear detectors. A plano-convex/concave lens can either modulate the aspect ratio of an image or create a line image from the point light beam source. A PCX cylindrical lens is also often hired to collect collimated light beams to generate a thin line.
Another crucial application of plano-convex/concave cylindrical lens is anamorphic beam shaping, which just refers to correcting the elliptical-shaped laser beam generated from a laser diode into a circular-shaped one. The elliptical laser beam is the consequence of a rectangular Fresnel aperture and is undesirable because this implies a larger beam area which wastes more power, fewer homogeneities, and a terrible Gaussian Beam Profile. A pair of plano convex/concave cylindrical lenses could be used to circularize the elliptical beams. During the test, a pair of plano-convex/concave cylindrical lenses are positioned so that lenses are orthogonal as shown in the figure. From the result, we can conclude that using a pair of plano-convex/concave cylindrical lenses to circularize the elliptical beam is a high-transmission, balance-shape, astigmatism-attenuated approach.
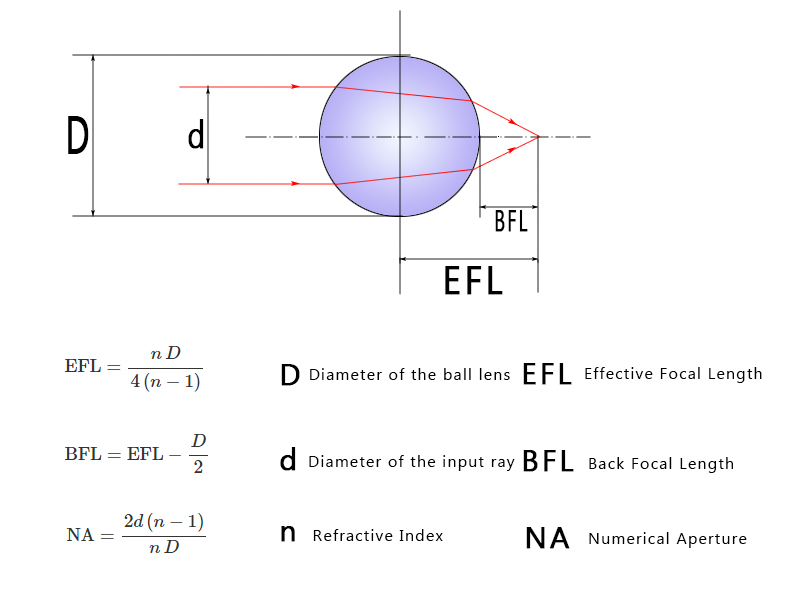
Ball Lenses are a special form of biconvex lenses which inherit the geometry of a ball (which implies completely spherical surfaces), manufactured from a single material with the optical transmission sited in the wavelength region of interest. The predominant function of ball lenses is light collimation/coupling for optical fibers (e.g. laser to fiber coupling, fiber to fiber coupling), with other versatile possibilities to be incorporated in miniature optics (e.g. Barcode Scanning, Sensors, or as objective lenses, etc.). Ball Lenses could also be considered as pre-forms aspheric lenses. One advantage of a ball lens is its short Back Focal Length (BFL), a trait that cuts down the distance from the optic to the fiber and is exceptionally useful when the installation space is rather tight, and compact dimension could simultaneously reduce the production cost. Additionally, a ball lens is rotationally symmetric, which enhances the ease of aligning and positioning.
Half-Ball Lenses are variants of ball lenses, obtained through simply cutting the ball lenses in half. Due to the ease of mounting brought by the one flat surface, half ball lenses are ideal for applications where more compact designs are required.
Rod Lenses are optical lenses in the form of a round rod and focus collimated beams into one dimension. Light is transferred against the circumference of the lens, therefore the circumferences of the rod lenses are precision polished, whilst the two flat ends are irrelevant to optical processing, but could be ground also. The uses of rod lenses include collimation of divergent light, linear focusing, and image inversion lenses between the objective and the ocular lenses in a rigid endoscope (An medical instrument to observe inside human bodies). A rod lens could also be utilized as a light pipe (An optical component that transfers light between the flat ends using total inter reflection.)

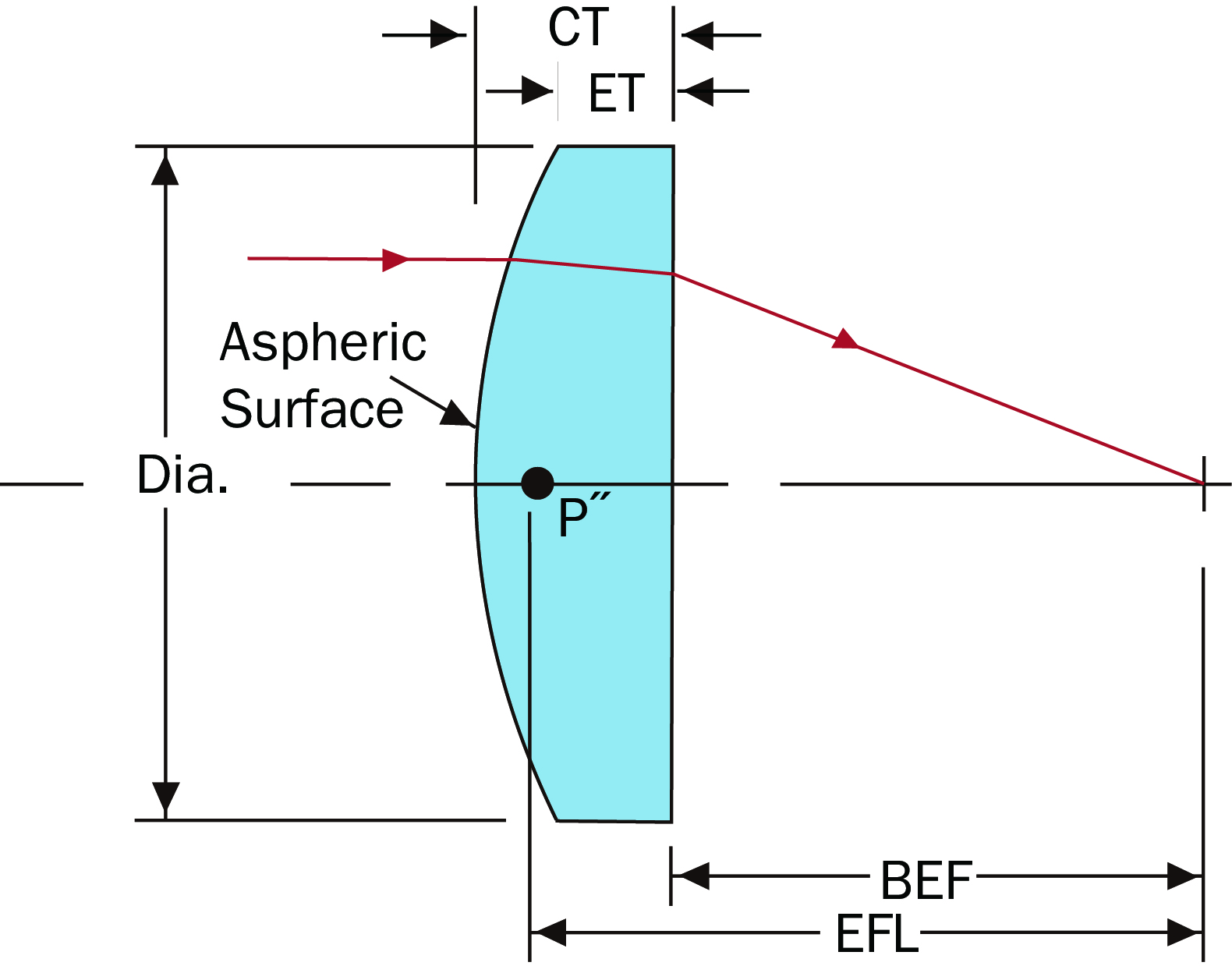
Aspheric Lens is an optical lens with the geometries of a non-spherical optical front (that is, the radius of curvature varies with the distance from the optical axis). The unique feature of an aspheric lens is the minimized spherical aberrations. Spherical aberrations intrinsic in spherical lenses, due to differences in the optical paths, the focal points of lights closer to the optical axis tend to be more forward than that of the lights incident at the edges of the spherical lenses, resulting in blurring of the image and increasing spot width. Compared with spherical lenses, Aspheric lenses exhibit spherical aberrations reduced to a dramatic extent, leading to enhanced image resolution, and spot diameters that are several orders less than the spot diameter of spherical lenses. An aspheric lens allows a larger numerical aperture (low f-number) and therefore increases the light throughput, achieving higher power efficiencies. Incorporation of aspheric lenses into lens modules also could help to reduce the element number with the exemption of excessive optics for correction of spherical aberrations, enabling compact and simplified design.
Axicons:
An Axicon or a Conical Lens is an optical lens with a conical side and flat side, it is defined by its base angles (referred to as the physical angles) and its apex angle. The working principle of an axicon is that it uses interference to create a focal line along the optical axis. Axicons could be utilized to generate an approximation of a diffraction-free Bessel beam, which is a beam consisting of a series of concentric rings having equal power through transforming collimated Gaussian beam in the near field. Although a Bessel beam does not exist in real life because it would require infinite energy to create, axicons offer a good analog by maintaining the non-diffractive Bessel beam properties over a distance much longer than a similar Gaussian beam. A plano-convex axicon could also be used to convert laser light into an annular shape by taking the projection in the far field, and the ring’s thickness will be 1/2 of the incident laser beam’s diameter.
![]()